
Plik z zadaniami do pobrania: 
Rachunek zdań
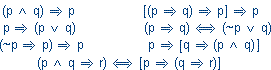
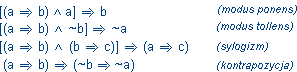
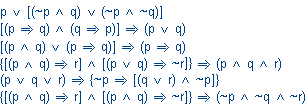
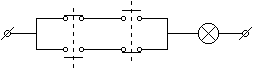 Dwie pary wyłączników sprzężonych tak, że w parze jeden jest włączony a drugi wyłączony, pozwalają, niezależnie od siebie, zaświecać i gasić żarówkę (zob. rys. obok). Napisz zdanie logiczne opisujące działanie tego obwodu. Przedstaw wartościowanie napisanego zdania. Udowodnij metodami rachunku zdań, że oba wyłączniki działają i ich działanie jest niezależne. (Sprawdź, że zanegowanie w zdaniu każdego z "wyłączników" z osobna daje taki sam wynik jak zanegowanie całego zdania.)
Dwie pary wyłączników sprzężonych tak, że w parze jeden jest włączony a drugi wyłączony, pozwalają, niezależnie od siebie, zaświecać i gasić żarówkę (zob. rys. obok). Napisz zdanie logiczne opisujące działanie tego obwodu. Przedstaw wartościowanie napisanego zdania. Udowodnij metodami rachunku zdań, że oba wyłączniki działają i ich działanie jest niezależne. (Sprawdź, że zanegowanie w zdaniu każdego z "wyłączników" z osobna daje taki sam wynik jak zanegowanie całego zdania.)
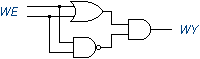 Bramkę XOR można przedstawić jako układ bramek: OR, NAND oraz AND (zob. rys. obok). Używając funktorów alternatywy, koniunkcji i negacji napisz zdanie logiczne opisujące działanie tego układu. Przedstaw wartościowanie napisanego zdania.
Bramkę XOR można przedstawić jako układ bramek: OR, NAND oraz AND (zob. rys. obok). Używając funktorów alternatywy, koniunkcji i negacji napisz zdanie logiczne opisujące działanie tego układu. Przedstaw wartościowanie napisanego zdania.
 ~ (a
~ (a b) nazywany jest dysjunkcją, funktorem Sheffera albo kreską Sheffera (zapis: a|b). Przedstaw tabelkę wartości tego funktora (por. bramkę NAND).
b) nazywany jest dysjunkcją, funktorem Sheffera albo kreską Sheffera (zapis: a|b). Przedstaw tabelkę wartości tego funktora (por. bramkę NAND).Funkcje zdaniowe
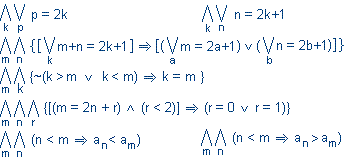
Algebra zbiorów
 A zdefiniuj zbiór pusty (0), równość i zawieranie (inkluzję) zbiorów, iloczyn, sumę i różnicę zbiorów oraz dopełnienie zbioru.
A zdefiniuj zbiór pusty (0), równość i zawieranie (inkluzję) zbiorów, iloczyn, sumę i różnicę zbiorów oraz dopełnienie zbioru.
 (A
(A B) = A A
B) = A A (A
(A B) = A
B) = A

 B, A
B, A B, A', A \ B, B \ A.
B, A', A \ B, B \ A.

 : –10
: –10 x
x 10},
A = {x
10},
A = {x Ω: x<0},
B = {x
Ω: x<0},
B = {x Ω: |x|
Ω: |x| 3};
3};
 : x
: x 20},
A = {x
20},
A = {x Ω: x
Ω: x 10},
B = {x
10},
B = {x Ω: x
Ω: x 15}.
15}.
 B) A = (A
B) A = (A B)
B) (A \ B)
(A \ B)
 (B \ C) = (A
(B \ C) = (A B) \ C
B) \ C B) \ C = (A \ C)
B) \ C = (A \ C) (B \ C)
(B \ C) (A
(A C)
C)
 B' = A' oraz B
B' = A' oraz B A, udowodnij, że A = B.
A, udowodnij, że A = B.

 (B \ A). Sprawdź, że:
(B \ A). Sprawdź, że: (A = B)
(A = B)
Zliczanie
Indukcja matematyczna i rekurencja
Relacje, własności relacji
 (B × C) = (A × B)
(B × C) = (A × B) (A × C)
(A × C) (B × C) = (A × C)
(B × C) = (A × C)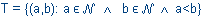
 A×A przedstaw w postaci diagramów:
A×A przedstaw w postaci diagramów: x < y;
x < y; x|y
x|y x ≠ y;
x ≠ y; 2|x + y.
2|x + y.
 X2, gdzie X = {a, b, c, d}:
X2, gdzie X = {a, b, c, d}:| 1 | 2 | 3 | 4 | 5 | |
| 1 | + | + | + | ||
| 2 | + | + | + | ||
| 3 | + | ||||
| 4 | + | + | + | ||
| 5 | + | + | + |
 R.
R.
 y| x; dla: x,y
y| x; dla: x,y
 \ {0}
\ {0}











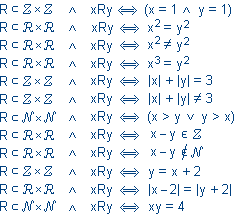
 x2 + y2 < 1
x2 + y2 < 1 x + y > 1
x + y > 1 (x = y) v (–x = y)
(x = y) v (–x = y) |x| < y
|x| < y X2 jest identycznością a R
X2 jest identycznością a R X2 dowolną relacją na zbiorze X. Pokaż, że:
X2 dowolną relacją na zbiorze X. Pokaż, że: IX jest słabo antysymetryczna.
IX jest słabo antysymetryczna.
Grafy
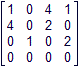 Narysuj graf, którego macierz sąsiedztwa przedstawiona jest obok. Jakie własności ma relacja, którą przedstawia graf? Jakie cechy grafu zawiązane są z własnościami relacji (takimi jak zwrotność, symetryczność, spójność ...)?
Narysuj graf, którego macierz sąsiedztwa przedstawiona jest obok. Jakie własności ma relacja, którą przedstawia graf? Jakie cechy grafu zawiązane są z własnościami relacji (takimi jak zwrotność, symetryczność, spójność ...)?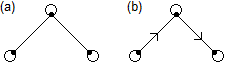 Napisz macierze sąsiedztwa grafów przedstawionych obok. Wypisz elementy relacji określonych przez te grafy. Jakie własności mają relacje określone przez te grafy? Czym różni się graf, macierz sąsiedztwa i relacja w przypadku (a) od grafu, macierzy sąsiedztwa i relacji w przypadku (b)?
Napisz macierze sąsiedztwa grafów przedstawionych obok. Wypisz elementy relacji określonych przez te grafy. Jakie własności mają relacje określone przez te grafy? Czym różni się graf, macierz sąsiedztwa i relacja w przypadku (a) od grafu, macierzy sąsiedztwa i relacji w przypadku (b)?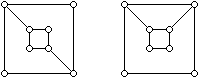 Wyjaśnij czemu nie są izomorficzne grafy:
Wyjaśnij czemu nie są izomorficzne grafy: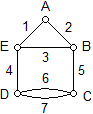 Wyznacz macierz sąsiedztwa i macierz incydencji grafu:
Wyznacz macierz sąsiedztwa i macierz incydencji grafu: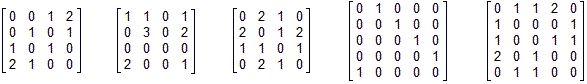
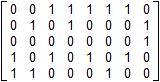 Narysuj graf, którego macierz incydencji jest:
Narysuj graf, którego macierz incydencji jest: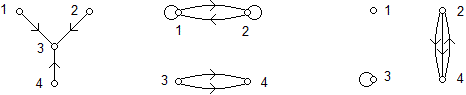 Wyznacz macierze grafów skierowanych:
Wyznacz macierze grafów skierowanych:Składanie relacji
 T.
T.Relacja równoważności
 X×X zbadaj, czy R jest relacją równoważności. Jeśli jest, wskaż klasy abstrakcji:
X×X zbadaj, czy R jest relacją równoważności. Jeśli jest, wskaż klasy abstrakcji: , xRy
, xRy x – y = 2;
x – y = 2; , xRy
, xRy x2
x2 y2;
y2; x + y ≠ 3;
x + y ≠ 3; 4| x2 – y2;
4| x2 – y2; \ {0}, xRy
\ {0}, xRy k| x + y (dla k
k| x + y (dla k
 );
); \ {0}, xRy
\ {0}, xRy k| x – y (dla k
k| x – y (dla k
 );
); \ {0}, xRy
\ {0}, xRy x·y jest liczbą nieparzystą;
x·y jest liczbą nieparzystą; \ {0}, xRy
\ {0}, xRy x·y = t2 (dla t
x·y = t2 (dla t
 );
); , xRy
, xRy x – y
x – y 
 ;
; A
A B v B
B v B A (gdzie Y jest ustalonym zbiorem co najmniej dwuelementowym, P(Y) oznacza zbiór wszystkich podzbiorów Y);
A (gdzie Y jest ustalonym zbiorem co najmniej dwuelementowym, P(Y) oznacza zbiór wszystkich podzbiorów Y); a
a (A
(A B) (gdzie a jest ustalonym elementem zbioru Y);
B) (gdzie a jest ustalonym elementem zbioru Y);
 X2. Zbadaj, czy są relacjami równoważności relacje określone następująco:
X2. Zbadaj, czy są relacjami równoważności relacje określone następująco: S, R
S, R S, X2 \ R.
S, X2 \ R. na dwa zbiory: zbiór liczb parzystych i nieparzystych. Wskaż relację równoważności, której klasami abstrakcji są te zbiory.
na dwa zbiory: zbiór liczb parzystych i nieparzystych. Wskaż relację równoważności, której klasami abstrakcji są te zbiory.
 ×
× na pięć zbiorów odpowiadających czterem ćwiartkom płaszczyzny i sumie osi wspolrzędnych Ox
na pięć zbiorów odpowiadających czterem ćwiartkom płaszczyzny i sumie osi wspolrzędnych Ox Oy. Znajdź relację równoważności, której klasami abstrakcji są te zbiory.
Oy. Znajdź relację równoważności, której klasami abstrakcji są te zbiory.
 ×
× dzielimy na zbiory będące okręgami o środkach w początku układu współrzędnych. Znajdź relację równoważności, której klasami abstrakcji są te zbiory.
dzielimy na zbiory będące okręgami o środkach w początku układu współrzędnych. Znajdź relację równoważności, której klasami abstrakcji są te zbiory.
Funkcje jako relacje
 oznacza zbiór wszystkich liczb rzeczywistych dodatnich. Zbadaj, która z podanych niżej relacji jest funkcją. Naszkicuj wykresy tych relacji.
oznacza zbiór wszystkich liczb rzeczywistych dodatnich. Zbadaj, która z podanych niżej relacji jest funkcją. Naszkicuj wykresy tych relacji.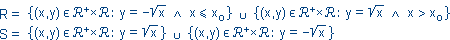

 ×
× , xRy
, xRy x2 = y2;
x2 = y2;
 +×
+× +, xRy
+, xRy x2 = y2;
x2 = y2;
 ×
× , xRy
, xRy x2 = y3;
x2 = y3;
 ×
× , xRy
, xRy x3 = y2;
x3 = y2;

 ×
× jako podzbiór płaszczyzny, podaj sens geometryczny tego iż:
jako podzbiór płaszczyzny, podaj sens geometryczny tego iż: —›
—› sprawdź czy jest ono:
sprawdź czy jest ono: —›
—›  określone wzorem: f(x) = 1 + int x.
określone wzorem: f(x) = 1 + int x. +).
+). , 2, 2
, 2, 2 } ).
} ).
 ×
× —›
—›  określone wzorem: f(n,k) = nk.
określone wzorem: f(n,k) = nk. × {2} ).
× {2} ). ×
× —›
—›  określone wzorem: f(x,y) = |x2 – y2|.
określone wzorem: f(x,y) = |x2 – y2|. \ Par) × Par), (Par: zbiór liczb parzystych).
\ Par) × Par), (Par: zbiór liczb parzystych). × {0} ).
× {0} ).
Relacje porządkujące
 (
( \ {0} )2 jest określona następująco:
xRy
\ {0} )2 jest określona następująco:
xRy 
 ( n
( n 

 nx = y ).
nx = y ). \ {0}, R) nie ma elementów maksymalnych.
\ {0}, R) nie ma elementów maksymalnych.
 ,
,  ,
,  są uporządkowane (częściowo, liniowo, dobrze) przez relację
są uporządkowane (częściowo, liniowo, dobrze) przez relację  (niewiększy).
(niewiększy).
 (inkluzji) częściowo porządkuje zbiór 2X.
(inkluzji) częściowo porządkuje zbiór 2X.

 }
}  {3} wraz z relacją | (podzielności).
{3} wraz z relacją | (podzielności).