Fizyka - zadania rachunkowe

• Kinematyka
• Dynamika
• Drgania i fale
• Elementy mechaniki kwantowej

Kinematyka

1. Pierwszą połowę drogi samochód przejechał z prędkością 40 km/h a drugą z prędkością 60 km/h. Jaka była średnia prędkość samochodu na całej drodze.
2. Z jakim przyspieszeniem porusza się obiekt, którego prędkość zależy od czasu następująco:
     a)   v = 3t + 2
     b)   v = – 2t + 100
     c)   v = t² + t + 1
     d)   v = – t³ – t² + 7
   Czy obiekt porusza się ruchem jednostajnym, jednostajnie przyspieszonym, opóźnionym?
3. Zależność drogi od czasu opisuje funkcja:
     a)   x = 2t² + t + 2
     b)   x = – 4t² – 2t + 1
     c)   x = 3t³ – 2t² – t
     d)   x = ½ at² + v_ot + x_o
     e)   x = 3 sin(2t + 2)
     f)    x = A sin(ωt + α)
   Znajdź funkcje opisujące prędkość i przyspieszenie.
4. Znajdź zależność położenia od czasu ciała poruszającego się prostoliniowo ze stałym przyspieszeniem a=const., korzystając jedynie z definicji: v=dx/dt, a=dv/dt.
5. Znajdź zależność prędkości i położenia od czasu w ruchu prostoliniowym jeśli ruch odbywa się ze stałym przyspieszeniem a=2 m/s² i prędkością początkową v=–2 m/s. Czy poruszające się ciało znajdzie się w początku układu współrzędnych jeśli położenie początkowe wynosiło x₀=1 m ?
6. Ciała A i B rozpoczęły spadek swobodny z tego samego punktu ale ciało B później o Δt niż ciało A. Znajdź zależność czasową odległości między nimi.
7. Ciało spada swobodnie na ziemię wewnątrz również spadającej swobodnie windy. Pokaż, że ciało nie porusza się względem windy lub jego ruch jest ruchem jednostajnym.
8. Punktowi materialnemu nadano prędkość początkową i dalej porusza się swobodnie w polu jednorodnym - np. w ziemskim polu grawitacyjnym w skali laboratoryjnej (tzw. rzut). Znajdź zależność prędkości i położenia tego punktu od czasu. Pokaż, że w ogólnym przypadku tor jego ruchu jest parabolą.
9. Na wysokości 1.5 m strzelono poziomo z łuku. Strzała wbiła się w ziemię w odległości 30 m. Jaki kąt tworzy z powierzchnią ziemi (przyjmując, że tor ruchu jest parabolą)?
10. Tor ruchu kamienia wyrzuconego ukośnie w górę jest parabolą. Napisz równanie tej paraboli jeśli wiadomo, że:
    - kamień rzucono pod kątem 45^o,
    - nad miejscem odległym od punktu wyrzutu o 4 m (poziomo) kamień osiągnął maksymalną wysokość równą 6 m.
    Odczytaj z równania paraboli informacje:
    - z jakiej wysokości wyrzucono kamień,
    - w jakiej odległości od punktu wyrzutu kamień znalazł się znowu na tej wysokości,
    - jaki był zasięg rzutu.
11. Punkt materialny porusza się po okręgu tak, że wartość jego prędkości pozostaje stała (tzw. ruch jednostajny po okręgu). Znajdź zależność położenia, prędkości i przyspieszenia od czasu. Wyraź te wielkości w prostokątnym (x,y) i biegunowym (r,φ) układzie współrzędnych.

na początek

Dynamika

12. Na równi poziomej znajdują się trzy klocki o masach m₁, m₂ i m₃ połączone linkami l₁ (klocek pierwszy z drugim) i l₂ (klocek drugi z trzecim) - jak na rysunku obok. Do pierwszego klocka została przyłożona poziomo siła F. Oblicz naprężenia linek łączących klocki:   (a)  zaniedbując tarcie klocków o równię,   (b)  uwzględniając to tarcie.
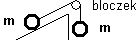13. Dwa ciała o jednakowych masach m połączono linką przerzuconą przez bloczek i umieszczono tak, że jedno spoczywa na równi pochyłej a drugie wisi swobodnie. Znajdź naprężenie linki. Kąt nachylenia równi wynosi 45^o.
    Dla uproszczenia przyjmij, że masa i rozciągliwość linki, masa bloczka i tarcie są zaniedbywalnie małe.
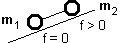14. Dwa ciała o masach m₁ i m₂, połączone nieważką i nierozciągliwą linką, zsuwają się po równi pochyłej o kącie nachylenia równym α. Współczynnik tarcia o równię ciała znajdującego się wyżej wynosi f, tarcie ciała znajdującego się niżej jest zaniedbywalnie małe.
    Znajdź naprężenie linki łączącej ciała.
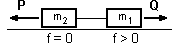15. Dwa ciała o masach m₁ i m₂ połączone linką (nieważką i nierozciągliwą) spoczywają na równi poziomej. Do pierwszego ciała przyłożono siłę Q, do drugiego siłę P (siły działają poziomo i P > Q). Współczynnik tarcia pierwszego ciała o podłoże wynosi f, drugiego jest zaniedbywalnie mały.
    Znajdź naprężenie linki łączącej ciała.
16. Kulę o masie m i promieniu R, obracającą się z prędkością kątową ω, delikatnie upuszczono na twardą i gładką poziomą płaszczyznę. Tarcie kuli o płaszczyznę powoduje spowalnianie obrotu kuli i równoczesnie zapoczątkowuje ruch postępowy kuli (toczenie się z poślizgiem). Po jakim czasie malejąca prędkość ruchu obrotowego i rosnąca prędkość ruchu postępowego 'uzgodnią się' i dalsze toczenie będzie się odbywać bez poślizgu?
    Współczynnik tarcia kuli o płaszczyznę jest równy f a moment bezwładności kuli względem jej środka I_o= 2/5 mR².
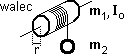17. Na walec nawinięto nieważką i nierozciągliwą nić. Koniec nici obciążono, na skutek czego odwija się ona (bez poślizgu) obracając walec wokół poziomej, nieruchomej osi pokrywającej się z osią symetrii walca. Walec ma promień r, masę m₁ i moment bezwładności I_o=½mr². Ciężarek ma masę m₂. Jakim ruchem obraca się walec, jakim ruchem obniża się ciężarek – podaj związek zachodzący pomiędzy nimi (które sformułowanie w treści zadania sugeruje, że ten związek istnieje?). Oblicz prędkość obrotu walca i naprężenie nitki.
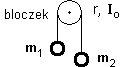18. Nieważką i nierozciągliwą linkę przerzucono przez bloczek o promieniu r i momencie bezwładności I_o. Oba końce linki obciążono ciężarkami o masach m₁ i m₂ (m₁ > m₂). Linka nie ślizga się po bloczku. Znajdź naprężenie linki jeśli:
       a) tarcie na osi bloczka jest zaniedbywalnie małe,
       b) moment siły tarcia na osi bloczka wynosi M_f.
19. Dane są trzy ciała, w kształcie sześcianu, walca i kuli. Walec i kula mają taki sam promień r a wszystkie trzy ciała jednakowe masy m. Wszystkie trzy jednocześnie puszczono swobodnie z trzech identyczych równi pochyłych (z tej samej wysokości), z których walec i kula staczają się bez poślizgu a sześcian zsuwa bez tarcia. W jakiej kolejności dane ciała dotrą do podstawy równi?
    Wskazówka: Moment bezwładności walca wynosi  I = 1/2 mr²  a kuli  I = 2/5 mr² (względem osi przechodzącej przez środek).
20. Dwie jednakowe kulki ślizgają się po gładkim, prostoliniowym, poziomym torze z prędkościami v₁ i v₂. Pokaż, że w wyniku zderzenia sprężystego (jednowymiarowego) kulki wymienią się prędkościami.
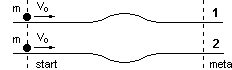21. Dane są dwa poziome tory, po których mogą się bez tarcia poruszać niewielkie kulki. Część środkowa pierwszego toru jest nieco wypukła, drugiego nieco wklęsła - przy czym wypukłość pierwszego toru dokładnie przystaje do wklęsłości drugiego (zob. rysunek obok). Poza tym oba tory są identyczne. W tym samym momencie, na starcie obu torów rozpoczęły ruch, z jednakowymi prędkościami początkowymi, dwie identyczne kulki, na które w trakcie ruchu działa tylko siła ciężkości. Masa i prędkość kulek są tak dobrane do krzywizny torów, że kulki toczą się gładko nie odrywając się od powierzchni toru. Która kulka szybciej pojawi się na mecie swojego toru?
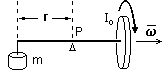22. Dźwignia dwustronna podparta jest w punkcie P (zob. rysunek obok). Na prawym ramieniu dźwigni zamocowane jest koło zamachowe, obracające się z prędkością kątową ω, którego moment bezwładności wynosi I_o. Lewe ramię, o długości r, obciążone jest masą m tak, że dźwignia pozostaje w równowadze. Jak zachowa się dźwignia po obciążeniu lewego ramienia dodatkową, niewielką masą  Δm?
    Wskazówka: Zastosuj II zasadę dynamiki w postaci  M_F = K. (dla ruchu obrotowego), gdzie M_F - moment siły, K - moment pędu (kręt). Pamiętaj, że są to wielkości wektorowe (zob: "różności / Precesja - przykład").
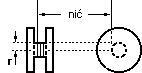23. Zabawka "jojo" podobna jest do krótkiej szpuli - dwie koliste tarcze połączone walcową osią, na którą nawinięta jest nić (zob. rysunek obok). Trzymając za koniec nici zaobserwujemy, że "jojo" będzie się obniżać, równocześnie obracając się i odwijając nić. Znając masę "jojo" m, jego moment bezwładności I_o względem osi symetrii obrotowej oraz promień r walca, na który nawinięta jest nić, oblicz z jakim przyspieszeniem "jojo" się obniża.
24. Przedstaw siły działające na pasażera  (1) przypieszającego autobusu,  (2) obracającej się karuzeli, z punktu widzenia:
    a)  obserwatora stojącego na ziemi (w inercjalnym układzie odniesienia),
    b)  pasażera (w nieinercjalnym układzie odniesienia).
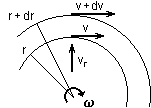25. Ciała spadające swobodnie na powierzchnię ziemi nie spadają pionowo - miejsce upadku odbiega od wskazanego przez pion opuszczony z punktu, z którego rozpoczął się spadek. Ten zadziwiający fakt świadczy o nieinercjalności układu odniesienia związanego z Ziemią, co jest skutkiem ruchu wirowego Ziemi. Znajdź przyspieszenie (wartość i kierunek) związane z tym efektem - tzw. przyspieszenie Coriolisa.
    Wskazówka: Weź pod uwagę poziomą tarczę, obracającą się ze stałą prędkością kątową ω. Zbadaj ruch ciała poruszającego się jednostajnie wzdłuż promienia tej tarczy, z prędkością v_r (zob. rysunek obok).
    Oszacuj średnią wartość przyspieszenia Coriolisa towarzyszącego swobodnemu spadkowi z wysokości 10 m (na równiku) i porównaj z wartością przyspieszenia ziemskiego. Czy dla tej skali zjawisk można uważać Ziemię za inercjalny układ odniesienia?
26. Pokaż, że równanie wyrażające II zasadę dynamiki jest niezmiennicze względem transformacji Galileusza (dla uproszczenia - w układzie jednowymiarowym).

na początek

Drgania i fale

27. Pokaż, że jeśli punkt porusza się po okręgu ze stałą prędkością kątową to jego rzut na średnicę wykonuje drgania harmoniczne.
28. Ciało wykonuje drgania harmoniczne opisane równaniem:  x(t) = 6 cos(3πt + π/3). Jakie jest jego położenie, prędkość i przyspieszenie w chwili t=2s. Znajdź też fazę, częstość kołową i okres drgań.
29. Ciało o masie  m  wykonuje ruch harmoniczny prosty o amplitudzie  A  i okresie  T. Znajdź siłę działającą na to ciało, podaj jej wartość maksymalną.
30. Korzystając z zależności:  x(t) = Asin(ωt),  oblicz maksymalną wartość energii kinetycznej i potencjalnej oscylatora harmonicznego. Oblicz sumę energii potencjalnej i kinetycznej swobodnego (nie tłumionego) oscylatora w dowolnej chwili i pokaż, że jest ona stała i równa maksymalnej wartości zarówno energii potencjalnej jak i kinetycznej (zasada zachowania energii dla oscylatora harmonicznego).
31. Zapisz energię mechaniczną  E  oscylatora harmonicznego jako sumę energii potencjalnej (zależnej od położenia  x) i kinetycznej (zależnej od prędkości). Sprawdź, że zasada zachowania enegii mechanicznej  (dE/dt = 0)  spełniona jest pod warunkiem, że działająca na oscylator siła jest wprost proporcjonalna do położenia  (F = –kx).
32. Napisz i rozwiąż równanie ruchu oscylatora harmonicznego swobodnego. Sprawdź rozwiązania postaci:  Asin(ωt),    Acos(ωt),    Ae^iωt,    Ae^–iωt.
33. Napisz równanie ruchu oscylatora harmonicznego tłumionego (siłą proporcjonalną do prędkości) i znajdź rozwiązanie w postaci:  x(t) = Ae^αte^iωt. Zinterpretuj otrzymane rozwiązanie. Pokaż, że przy braku tłumienia rozwiązanie redukuje się do rozwiązania oscylatora swobodnego.
34. Napisz równanie ruchu oscylatora harmonicznego wymuszonego. Dla siły wymuszającej:  F = F_oe^iωt  przyjmij rozwiązanie w postaci:  x(t) = Ae^iωt  i oblicz amplitudę drgań. Przedyskutuj rozwiązanie w zależności od różnicy częstości: siły wymuszającej i drgań własnych.
35. Napisz równanie ruchu oscylatora harmonicznego wymuszonego siłą  F = F_oe^iωt  i tłumionego siłą proporcjonalną do prędkości. Oblicz zespoloną amplitudę drgań i zinterpretuj otrzymany wynik. Jaki będzie rzeczywisty wynik pomiaru amplitudy?
36. Sprawdź, że każda z funkcji:
    (a)   Ψ(x,t) = Acos(kx–ωt);     (b)   Ψ(x,t) = Asin(kx–ωt);     (c)   Ψ(x,t) = Ae^{i (kx–ωt)};
    jest rozwiązaniem równania fali biegnącej (jednowymiarowej):
    ∂²Ψ/∂x² = (1/v²) ∂²Ψ/∂t².
    Oblicz "przy okazji" prędkość fali  v.
37. Znajdź amplitudę sumy dwóch fal jednowymiarowych, których amplitudy są jednakowe a częstości różnią się nieznacznie. Znajdź wyrażenie na prędkość przemieszczania się (wzdłuż kierunku rozchodzenia się fali) "miejsc" o stałej (np. maksymalnej) amplitudzie drgań - prędkość grupową.
38. Oblicz trzy kolejne częstości drgań harmonicznych (odpowiadające trzem kolejnym, coraz krótszym falom stojącym) dla struny zamocowanej na obu końcach oraz dla struny (pręta) zamocowanej na jednym końcu. Częstość drgań podstawowych wynosi w obu wypadkach ω_o.

na początek

Elementy mechaniki kwantowej

39. Pokaż, że warunek kwantowy Bohra nałożony na orbity elektronu w atomie wodoru równoważny jest warunkowi istnienia na tych orbitach fal stojących de Broglie'a związanych z elektronem.
40. Przyspieszoną napięciem U wiązkę elektronów skierowano na cienką warstwę substancji krystalicznej i po przejściu zarejestrowano na kliszy fotograficznej. Odległość kliszy od warstwy krystalicznej wynosiła d. Na otrzymanym zdjęciu można zidentyfikować szereg punktów leżących na okręgu o promieniu r. Podaj wyrażenie pozwalające oszacować odległość między atomami w prześwietlanym elektronami krysztale.
41. Cząstka o masie m "uwięziona" jest w obszarze o niewielkich rozmiarach. Dla uproszczenia weź pod uwagę jednowymiarowy ruch cząstki przyjmując, że może się poruszać tylko wzdłuż odcinka o długości a. Znajdź dopuszczalne wartości pędu tej cząstki.
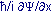42. Operator pędu działający na funkcję falową Ψ dany jest w postaci: . Korzystając z klasycznego związku między energią i pędem:  E=p²/2m  podaj postać operatora energii.
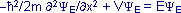43. Dane jest równanie Schrödingera (jednowymiarowe) przedstawiające całkowitą energię E cząstki w stanie opisanym funkcją Ψ_E. Pokaż, że jeśli cząstka jest swobodna, tzn. jej energia potencjalna V=0, to funkcja  Ψ_E = Ae ^{i (kx–ωt)}  spełnia to równanie. Sprawdź, że energia E cząstki swobodnej może przyjmować dowolne wartości (nie jest skwantowana).

na początek