Algebra liniowa i geometria analityczna - zadania
WERSJA NIEOFICJALNA


    Liczby zespolone
  1. Rozwiąż równania:
    x2 + 4x + 8 = 0     2x2 + 4x + 4 = 0     x2 – 4x + 5 = 0     3x2 – 30x + 87 = 0
    x2 – x + ½ = 0      ½x2 – 2x + 2¼ = 0
  2. Podane liczby przedstaw w postaci trygonometrycznej i wykładniczej:
    + i,       –– i,       2 + 2i,       2 – 2i,       3 + 3i,       –3 + 3i.
  3. Oblicz sumy, różnice, iloczyny i ilorazy poniższych par liczb:
    a + bi,  a – bi;       exp(2πi),  i;         1 – i,  exp(πi);         2 – 3i,  3 – 2i;         –3 – i,  3 + i;
    2[cos(π/3) + i sin(π/3)],  cos(π/2) + i sin(π/2);         2 exp(iπ/2),  3 exp(iπ/6).
  4. Oblicz pierwiastki kwadratowe z liczb:
    4 – 4i,       –2 + 2i,       2 – 2i,       –1 + i,       4 + 3i.
  5. Oblicz pierwiastki stopnia 2 i 3 z liczby i.
  6. Oblicz pierwiastki stopnia 3, 4 i 8 z liczby 1.
  7. Korzystając z własności liczb zespolonych, przedstaw każdą z funkcji wielokrotności kąta: sin 3φ,  cos 3φ,  sin 6φ,  cos 6φ,  używając funkcji pojedynczego kąta:  sin φ,  cos φ.
  8. Kiedy kwadrat liczby  a + bi  jest liczbą:
        rzeczywistą,
        ujemną,
        urojoną?
  9. Jakie muszą być argumenty liczb z1 z2 (różnych od zera) aby:
        iloczyn  z1z2  był liczbą rzeczywistą,
        iloraz  z1/z2  był liczbą rzeczywistą?
  10. Pokaż, że:     = + ,       = ,       = / .
  11. Pokaż, że:     1/z = / |z|2
  12. Rozwiąż równania:     z + (z – ) = 3 + 2i,            i(z + ) + i(z – ) = 2i – 3.
  13. Rozwiąż równania:     (1 + i)x + (2 – i)y = 2 – 2i,     (1 – i)x – (3 + i)y = –3 + 3i
  14. Jakie twory geometryczne określają następujące równania i nierówności:
    |z| = 1,     0 < |z – 1| < 1,     |z – i| < ½,     |z2 – 1| = 1.

    15. na początek

    Układy równań liniowych.

  15. Napisz macierz układu równań, znajdź macierz odwrotną i sprawdź, że mnożąc ją przez wektor wyrazów wolnych otrzymasz rozwiązanie:
  16. Rozwiąż układy równań metodą Cramera:
  17. Rozwiąż układy równań z poprzedniego zadania, metodą Gaussa.
  18. Rozwiąż układy równań metodą Gaussa:
  19. Zbadaj ile rozwiązań ma układ równań w zależności od parametru m (posłuż się metodą Cramera):
    mx +  y +  z = 1
     x + my +  z = m
     x +  y + mz = m2

    na początek

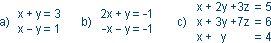
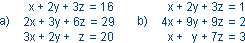
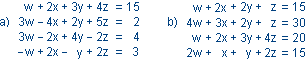
    Własności macierzy.

  20. Udowodnij, że transponowanie macierzy nie zmienia wartości wyznacznika:   det A = det AT
  21. Udowodnij, że permutacja nieparzysta wierszy lub kolumn macierzy zmienia znak wyznacznika tej macierzy, natomiast permutacja parzysta – nie zmienia.
  22. Pokaż (na przykładzie macierzy 2x2 i 3x3), że:   det (AB) = det (BA)
  23. Pokaż (na przykładzie macierzy 2x2 i 3x3), że iloczyn wyznaczników macierzy równy jest wyznacznikowi iloczynu tych macierzy:   det (AB) = det A det B
  24. Pokaż (na przykładzie macierzy 2x2), że wyznacznik macierzy nieosobliwej równy jest odwrotności wyznacznika macierzy odwrotnej:   det A = (det A–1)–1
  25. Pokaż (na przykładzie macierzy 2x2 i 3x3), że jeśli dowolny wiersz macierzy zastąpić sumą tego wiersza i dowolnego innego wiersza pomnożonego przez stałą rzeczywistą, to wyznacznik macierzy nie zmieni się. Udowodnij, że jeśli powyższa własność wyznacznika prawdziwa jest dla wierszy to jest prawdziwa również dla kolumn macierzy.
  26. Udowodnij a następnie sprawdź na przykładzie macierzy 2x2 i 3x3, że jeśli dowolny wiersz lub kolumnę danej macierzy pomnożyć przez liczbę rzeczywistą, to wyznacznik otrzymanej w ten sposób nowej macierzy, równy jest wyznacznikowi macierzy danej pomnożonemu przez tę liczbę.
  27. Pokaż bez obliczania wyznaczników, że poniższe macierze są osobliwe:
  28. Sprawdź czy poniższe macierze są nieosobliwe, jeśli tak znajdź ich macierze odwrotne. Sprawdź na wybranym przykładzie, że próba odwrócenia macierzy osobliwej prowadzi do sprzecznego układu równań. Sprawdź przemienność mnożenia macierzy przez macierz odwrotną.

    na początek

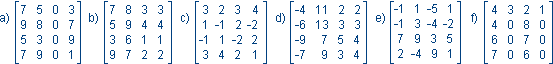
    Przekształcenia liniowe.

  29. Znajdź (w trójwymiarowej przestrzeni kartezjańskiej) macierz obrotu wokół osi OZ. Oblicz współrzędne wektora w' w jaki przekształci się po takim obrocie wektor:
        a)  w = (2, 1, 0)
        b)  w = (1, 1, 4)
    Sprawdź, że długość wektora jest niezmiennikiem obrotu. Czy wektory w i w' są prostopadłe?
  30. Znajdź macierze obrotu wokół osi OX, OY i OZ o kąt 45°.
  31. Napisz macierze obrotu wokół osi OZ o kąt 45° w prawo a następnie w  lewo. Złożenie obu obrotów jest oczywiście przekształceniem tożsamościowym - pokaż, że iloczyn napisanych macierzy obrotów jest macierzą przekształcenia tożsamościowego (jednostkową).
  32. Znajdź macierze przekształceń będących złożeniami obrotu wokół osi OY o kąt 30° i wokół osi OZ o kąt 60° (w różnej kolejności). Przy pomocy znalezionych macierzy przekształć dowolny wektor i pokaż na tym przykładzie, że składanie obrotów jest nieprzemienne.
  33. Znajdź współrzędne wektora w' w jaki przekształci się wektor w = (2, 0, 0) w wyniku obrotu wokół osi OZ o 90° i jednoczesnego dwukrotnego wydłużenia. Napisz macierz odpowiedniego przekształcenia.
  34. Znajdź współrzędne wektora w' w jaki przekształci się wektor w = (1, 1, 1) w wyniku obrotu o 45° wokół osi OX, połączonego z obrotem o 30° wokół osi OY z jednoczesnym skróceniem o 25%. Napisz macierz odpowiedniego przekształcenia.

    na początek

    Geometria analityczna.

  35. Napisz współrzędne trzech dowolnych punktów A, B i C, nie leżących na tej samej prostej. Znajdź współrzędne wszystkich wektorów łączących te punkty. Oblicz pole trójkąta ABC, stosując iloczyn wektorowy - powtórz obliczenie kilkakrotnie, biorąc różne pary wektorów. Znajdź miary boków i kątów trójkąta ABC.
  36. Napisz równanie prostej przechodzącej przez punkt (1,1,1) i równoległej
    a)  do osi OX,
    b)  do osi OY,
    c)  do osi OZ.
  37. Napisz współrzędne dwóch dowolnych punktów A i B. Znajdź równanie prostej przechodzącej przez te punkty. Napisz współrzędne kilku innych punktów leżących na tej prostej.
  38. Trzy krawędzie sześcianu wychodzące ze wspólnego wierzchołka pokrywają się z osiami układu współrzędnych. Napisz równania wszystkich prostych wyznaczonych przez
    a)  krawędzie sześcianu,
    b)  przekątne ścian sześcianu,
    c)  przekątne objętościowe sześcianu.
  39. Napisz równanie płaszczyzny:
    a) przechodzącej przez punkt 1 na osi OX i równoległej do płaszczyzny YZ,
    b) przechodzącej przez punkt 1 na osi OY i równoległej do płaszczyzny XZ,
    c) przechodzącej przez punkt 1 na osi OZ i równoległej do płaszczyzny XY.
  40. Napisz równanie płaszczyzny przechodzącej przez punkty A, B i C.
    a)  A (1,2,2),     B (–1,1,0),    C(3,1,1);
    b)  A (4,1,0),     B (1,1,1),     C (2,1,4);
    c)  A (1,1,5),     B (5,2,2),     C (0,1,5);
    d)  A (2,1,1),     B (1,2,3),     C (1,–1,–1).
  41. Trzy krawędzie sześcianu wychodzące ze wspólnego wierzchołka pokrywają się z osiami układu współrzędnych. Napisz równania wszystkich płaszczyzn wyznaczonych przez ściany tego sześcianu. Napisz równania płaszczyzn wyznaczonych przez pary równoległych przekątnych przeciwległych ścian.

    Poniższe dane są wspólne dla kolejnych zadań:

    - płaszczyzna przechodząca przez punkt A i równoległa do wektorów a i b,
    - prosta przechodząca przez punkt C i równoległa do wektora c,
    - punkt D:

    1. płaszczyzna:   A (0,0,0),   a = (1,0,1),   b = (0,1,0)
      prosta:   C (0,1,2),   c = (–1,0,1)
      punkt:   D (1,1,1)
    2. płaszczyzna:   A (0,0,1),   a = (1,0,0),   b = (0,2,0)
      prosta:   C (1,1,0),   c = (0,0,1)
      punkt:   D (0,1,0)
    3. płaszczyzna:   A (1,0,0),   a = (1,–1,0),   b = (2,0,0)
      prosta:   C (0,0,2),   c = (1,1,0)
      punkt:   D (0,0,0)
    4. płaszczyzna:   A (0,1,0),   a = (1,–1,0),   b = (1,0,0)
      prosta:   C (–1,0,1),   c = (1,0,0)
      punkt:   D (1,1,–1)
    5. płaszczyzna:   A (1,1,1),   a = (1,1,1),   b = (–1, 1, 1)
      prosta:   C (3,1,0),   c = (–1,–1, 1)
      punkt:   D (1,1,–1)
  42. Znajdź wektor jednostkowy prostopadły do danej płaszczyzny.
  43. Znajdź kąty utworzone przez pary danych płaszczyzn.
  44. Znajdź kąty utworzone przez pary danych prostych.
  45. Znajdź kąt jaki tworzy dana prosta z daną płaszczyzną.
  46. Znajdź prostą prostopadłą do danej płaszczyzny przechodzącą przez dany punkt D.
  47. Znajdź punkt P, w którym dana prosta przebija daną płaszczyznę.

    na początek