Teoria niepewności pomiaru
Nie istnieją pomiary bezbłędne, których wyniki są absolutnie dokładne i pewne! Każdy wynik realnego pomiaru zawiera błąd, którego wielkość zależy od techniki pomiaru i dokładności użytych przyrządów (np. długość można zmierzyć zwykłym przymiarem z dokładnościa do 1 mm, suwmiarką – do 0.1 mm, śrubą mikrometryczną – do 0.01 mm). Oprócz tego, nawet jeśli powtórzymy starannie pomiar tą samą metodą i tym samym przyrządem, możemy otrzymać różne wyniki, z powodów, których nie da się do końca wyeliminować ani nawet przewidzieć (np. różnice w pomiarach śrubą mikrometryczną średnicy drutu, spowodowane niejednorodnością samego drutu).
Błędy można podzielić na:
Skutkiem wpływu na wynik pomiaru wszystkich pojawiających się podczas pomiaru błędów przypadkowych jest niepewność pomiaru.
Jak radzić sobie z błędami przypadkowymi i wynikającą z nich niepewnością pomiaru?
Przede wszystkim pomiary należy powtarzać – pojedynczy wynik pomiaru nie zawiera wiarygodnej informacji o wielkości mierzonej. Jeśli powtarzając pomiar otrzymujemy jednakowe wyniki, to niepewność pomiaru jest mniejsza od dokładności użytego przyrządu i można ją pominąć przy ocenie dokładności pomiaru. Dokładność pomiaru jest wtedy równa dokładności przyrządu (np. klasie miernika elektrycznego).
Co robić, jeśli jednak, pomimo największej staranności, powtarzane pomiary dają różne wyniki? Pozostają do wykorzystania metody statystyczne, co oczywiście oznacza, że pomiar należy powtórzyć wielokrotnie.
Rozważmy przykład wielokrotnego (ponad 1000 razy) pomiaru pewnej wielkości (wyniki zostały wygenerowane numerycznie i niepewność pomiaru jest przesadnie wielka).
Tabela 1. Uporządkowane wyniki wielokrotnego pomiaru pewnej wielkości (*)
| wynik pomiaru | częstość | wynik pomiaru | częstość | wynik pomiaru | częstość | ||
| 36 | 1 | 46 | 89 | 56 | 75 | ||
| 37 | 1 | 47 | 155 | 57 | 62 | ||
| 38 | 6 | 48 | 168 | 58 | 37 | ||
| 39 | 11 | 49 | 185 | 59 | 20 | ||
| 40 | 12 | 50 | 181 | 60 | 11 | ||
| 41 | 24 | 51 | 193 | 61 | 6 | ||
| 42 | 29 | 52 | 165 | 62 | 2 | ||
| 43 | 38 | 53 | 156 | 63 | 1 | ||
| 44 | 71 | 54 | 113 | 64 | 4 | ||
| 45 | 90 | 55 | 94 |
*) dane wygenerowane programem Galton z serwisu "Wirtualny Wszechświat, modelowanie rzeczywistości": ( www.wiw.pl/modelowanie )
Uporządkowane wyniki zawiera lewa kolumna tabeli 1. Po zaobserwowaniu, że wyniki pomiaru powtarzają się, ilość powtórzeń (częstość) każdego wyniku zapisano w prawej kolumnie tabeli 1. Niektóre wyniki pojawiały się częściej inne rzadziej i tak np. wynik "50" pojawił się 181 razy, "51" – 193 razy, "60" – 11 razy a "63" – tylko 1 raz.
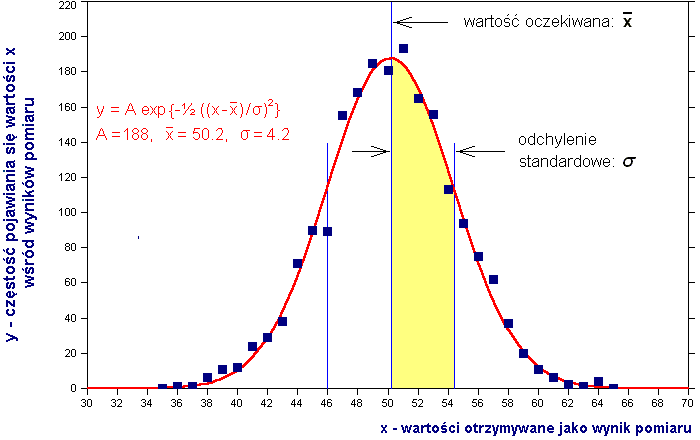
Opracowanie otrzymanych wyników zacznijmy od narysowania rozkładu częstości pojawiania się poszczególnych wyników (zob. rys. 1):

Rys. 1. Rozkład częstości wyników pomiaru – rozkład Gaussa.
Na osi poziomej zaznaczono wszystkie wartości otrzymywane jako wyniki pomiaru, na pionowej – częstość pojawiania się poszczególnych wartości wśród otrzymanych wyników.
Jaki użyteczny wynik otrzymano z tych pomiarów i z jaką dokładnością?
Zauważmy najpierw, że częstości pojawiania się różnych wyników pomiaru rozkładają się dość regularnie wzdłuż krzywej, zwanej czasem, ze względu na kształt, krzywą dzwonową. Jeśli błędy pomiaru są rzeczywiście przypadkowe a ilość wyników pomiaru rośnie, to rozkład częstości zmierza do rozkładu Gaussa:
y = A e–½ (( x – x–) / σ )2
gdzie: A - wysokość krzywej w maksimum, x–- położenie maksimum, σ - odchylenie standardowe (odległość punktu przegięcia od maksimum krzywej, mierzona wzdłuż osi x).
Jaki jest związek parametrów krzywej Gaussa z użytecznym wynikiem pomiaru?
Można się spodziewać, że "najlepszą" wartością otrzymaną w wyniku wielokrotnego pomiaru jest ta, która pojawia się z największą częstością. Ściśle rzecz biorąc, tę "najlepszą" wartość, zwaną wartością oczekiwaną, wskazuje położenie maksimum krzywej Gaussa, przy czym wartość oczekiwana nie musi pokrywać się z żadnym pojedynczym wynikiem pomiaru lecz jest reprezentatywna dla całej serii pomiarów (zob. rys. 1).
Jak można ocenić dokładność serii pomiarów?
Czym dokładniejsze pomiary w serii, tym mniej różnią się one od wartości oczekiwanej (mają mniejszy rozrzut) a zatem krzywa Gaussa jest węższa (w przypadku pomiaru idealnie dokładnego wszystkie wyniki byłyby jednakowe i równe wartości oczekiwanej). W pomiarach mniej dokładnych pojawia się więcej wyników odbiegających od wartości oczekiwanej – krzywa Gaussa jest szersza. Dobrą miarą niepewności pomiaru jest więc, związane z szerokością krzywej, odchylenie standardowe.
Dla dokładniejszego określenia związku między odchyleniem standardowym a niepewnością pomiaru, na wykres krzywej Gaussa, symetrycznie wokół maksimum, zostały naniesione odcinki o długości odpowiadającej pojedynczemu, podwójnemu i potrójnemu odchyleniu standardowemu σ, tworząc przedziały, których środkiem jest wartość oczekiwana x–(zob. rys. 2):

Rys. 2. Odchylenia wyników pomiaru na tle krzywej Gaussa.
Jaka część wszystkich wyników pomiaru mieści się w każdym z przedziałów?
Miarą ilości wyników pomiaru zawartych w wybranym przedziale jest pole ograniczone wykresem krzywej Gaussa w tym przedziale – można je obliczyć jako całkę oznaczoną z funkcji Gaussa w tymże przedziale. Należy obliczyć (lub oszacować numerycznie) całkę oznaczoną w granicach [–∞, +∞] i całki oznaczone w granicach z rys. 2. Porównując wyniki i traktując wartość całki z przedziału [–∞, +∞] jako 100% (albowiem w tym przedziale z pewnością muszą być zawarte wszystkie wyniki pomiaru) stwierdzimy, że w przedziale [x–– σ, x–+ σ] powinno znaleźć się około 68,5% wszystkich wyników pomiaru natomiast w przedziale [x–– 3σ, x–+ 3σ] – ponad 99,7% (zob. rys. 2).
Wynik ten można interpretować w kategoriach prawdopodobieństwa:
Skoro w przedziale [x–– σ, x–+ σ] zawiera się 68,5% wszystkich wyników pomiaru, zatem wybrany losowo wynik, z takim właśnie prawdopodobieństwem będzie pochodzić z tego przedziału. Innymi słowy, odchylenie pojedynczego pomiaru od wartości średniej nie przekroczy odchylenia standardowego, z prawdopodobieństwem 68,5%. Podobnie wnioskujemy, że odchylenie pojedynczego pomiaru nie przekroczy trzech odchyleń standardowych, z prawdopodobieństwem większym niż 99,7% czyli bardzo bliskim pewności. Dlatego, w teorii niepewności pomiaru, trzy odchylenia standardowe interpretuje się jako odchylenie maksymalne serii pomiarów (jest to dobre przybliżenie gdyż na każdy 1000 pomiarów, przeciętnie mniej niż trzy wyniki mogą mieć większe odchylenie).
Czy można zmniejszyć odchylenie serii pomiarów?
Jedynym sposobem jest wielokrotne, staranne powtórzenie pomiaru. Im więcej dokładnych pomiarów, niewiele różniących się od wartości średniej, będzie zawierała seria, tym mniejsze będzie odchylenie serii.
Trzeba pamiętać, aby przed statystycznym opracowniem serii wyników pomiaru, upewnić się, że nie został popełniony błąd systematyczny. Wtedy bowiem wartość oczekiwana może być obarczona błędem, który nie ma wpływu na odchylenie standardowe, np. seria identycznych wyników (zerowe odchylenie standardowe) pomiaru czasu wykonanych "spóźniającym się" stoperem (wszystkie wyniki zaniżone).
Czy za każdym razem trzeba sporządzać rozkład częstości wyników pomiaru w serii a następnie dopasowywać do niego krzywą Gaussa aby otrzymać wartość oczekiwaną i odchylenie standardowe?
Dokładne wartości parametrów krzywej Gaussa można zastąpić estymatorami tych parametrów, czyli ich wartościami przybliżonymi. Można je obliczyć bez pracochłonnego sporządzania rozkładu częstości i dopasowywania krzywej Gaussa.
Estymatorem wartości oczekiwanej x–jest średnia arytmetyczna, odchylenia standardowego σ - odchylenie średnie kwadratowe:
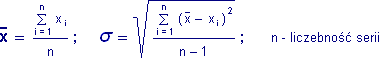
W praktyce, najwygodniej jest obliczyć wartość średnią i odchylenie standardowe, korzystając z "gotowych" funkcji, np. dowolnego arkusza kalkulacyjnego.
Przykład:
Dwaj eksperymentatorzy zmierzyli wielokrotnie (42 razy) wartość przyspieszenia ziemskiego. Otrzymane przez nich serie wyników, umownie nazwane [a] i [b], uporządkowane malejąco ze względu na częstość, pokazano niżej:
seria [a]: 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 9.6; 9.6; 9.6; 9.6; 9.6; 9.6; 9.6; 10.2; 10.2; 10.2; 10.2; 10.2; 10.2; 10.2; 9.4; 9.4; 9.4; 10.4; 10.4; 10.4; 9.2; 10.6.
seria [b]: 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 9.8; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 10.0; 9.6; 9.6; 9.6; 9.6; 9.6; 9.6; 10.2; 10.2; 10.2; 10.2; 10.2; 10.2; 9.4; 9.4; 9.4; 9.4; 10.4; 10.4; 10.4; 10.4; 9.2; 9.2; 10.6; 10.6; 9.0; 10.8.
Jaką wartość przyspieszenia ziemskiego otrzymał każdy z eksperymentatorów i jaka była dokładność ich pomiarów?
Obliczając średnią arytmetyczną, przy pomocy funkcji ŚREDNIA arkusza Excel (jako estymatora wartości oczekiwanej), otrzymujemy, zarówno dla serii [a] jak i serii [b] ten sam wynik: x–= 9,9.
Odchylenia standardowe obliczone przy pomocy funkcji ODCH.STANDARDOWE (zaokrąglone do części dziesiątych), wynoszą odpowiednio: σ[a] = 0,3 oraz σ[b] = 0,4. Daje to maksymalne odchylenie serii [a] (maksymalny "rozrzut" pomiarów w serii): ± 0,9; nbsp;serii [b]: ± 1,2 – pierwszy eksperymentator mierzył staranniej.
Na rys. 3 przedstawiono, dla porównania, częstości wyników pomiaru dla obu serii i opisane na nich krzywe Gaussa wraz z wartościami parametrów dającymi najlepsze dopasowanie:
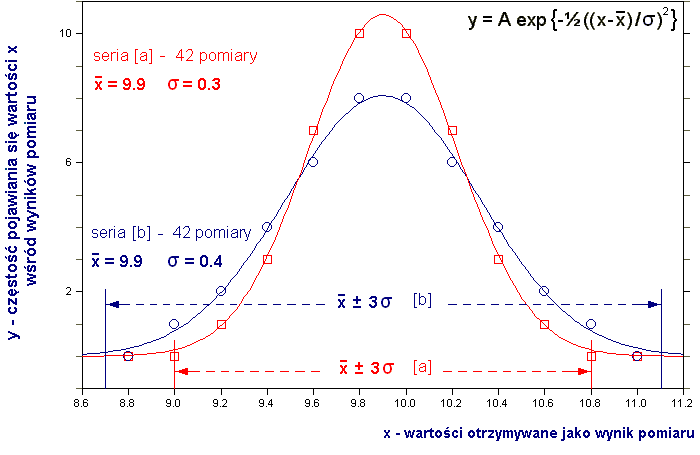
Rys. 3. Krzywe Gaussa opisane na dwóch niezależnych seriach [a] i [b] pomiarów różniących się dokładnością.
Widać, że wartości oczekiwane i odchylenia standardowe obu serii, otrzymane jako parametry krzywych Gaussa, są identyczne z obliczonymi wcześniej, przy użyciu odpowiednich funkcji arkusza kalkulacyjnego.
Dotąd przedstawiono sposób znajdowania wartości oczekiwanej, która jest użytecznym wynikiem serii pomiarów, oraz odchylenia standardowego i maksymalnego serii. Dla eksperymentatora ważna jest jednak przede wszystkim niepewność wartości oczekiwanej, czyli dokładność użytecznego wyniku pomiarów.
Jaka jest niepewność wartości oczekiwanej?
Wartość oczekiwaną serii pomiarów wielkości x, składającej się z n pomiarów, można obliczyć jako średnią arytmetyczną:
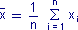
Jest to więc funkcja n zmiennych (wyników pomiaru): x1, x2, ... xn. Obliczmy niepewność średniej arytmetycznej jako jej różniczkę zupełną:
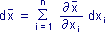
Ponieważ średnia arytmetyczna zależy w ten sam sposób od wszystkich składników, więc wszystkie pochodne cząstkowe również są takie same:
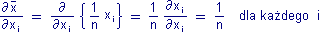
Po uwzględnieniu obliczonych pochodnych cząstkowych i zastąpieniu różniczek dxi odchyleniami Δxi, różniczka zupełna średniej arytmetycznej przekształci się w następującą zależność niepewności wartości średniej (oczekiwanej) od odchyleń poszczególnych pomiarów:

Jak oszacować sumę odchyleń wszystkich pomiarów: Σ Δxi = ?
Iloczyn odchylenia maksymalnego przez ilość pomiarów da na pewno o wiele za dużą wartość - praktycznie wszystkie pomiary mają odchylenie mniejsze od odchylenia maksymalnego: Σ Δxi << n.3σ. Iloczyn odchylenia standardowego przez ilość pomiarów też da wartość z nadmiarem - ponad połowa (68,5%) pomiarów ma mniejsze odchylenie: Σ Δxi < n.σ (zob. rys. 2).
Zastosujmy następujący chwyt: skoro niepewność wartości średniej chcemy wyrazić przez odchylenie standardowe serii, a estymatorem odchylenia standardowego jest odchylenie średnie kwadratowe, to obliczmy sumę kwadratów odchyleń:
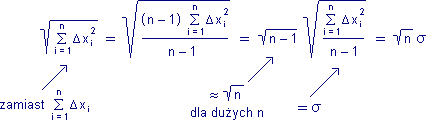
Podstawiając otrzymany wynik zamiast Σ Δxi , do wyrażenia na zależność niepewności wartości średniej Δx–od odchyleń Δxi poszczególnych pomiarów, otrzymujemy wielkość, która jest miarą niepewności wartości średniej (ale oczywiście nie jest różniczką zupełną):
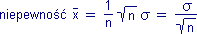
Wielkość ta nazywana jest niepewnością standardową wartości średniej (błędem standardowym wartości średniej) i zależy od odchylenia standardowego σ oraz liczebności n serii pomiarów:

Niepewność standardową wartości średniej można interpretować w kategoriach prawdopodobieństwa, tak jak odchylenie standardowe σ serii pomiarów. Można wobec tego z prawdopodobieństwem 68,5% (zob. rys. 2) przyjąć, że średnia serii pomiarów, nie różni się więcej niż o niepewność standardową od nieznanej wartości prawdziwej. Biorąc trzykrotność odchylenia standardowego czyli odchylenie maksymalne serii pomiarów (zob.rys. 2), otrzymamy niepewność maksymalną wartości średniej serii pomiarów.

Dokładność wyniku eksperymentu fizycznego zazwyczaj podaje się w postaci niepewności maksymalnej - stosując ten rodzaj niepewności można o tym nie informować (jest to "ustawienie domyślne"). Podając dokładność wyniku eksperymentu w inny sposób - trzeba ten sposób określić.
© marpaw'05-10